Rで一般化加法モデル（GAM）を使う

Rで一般化加法モデル（GAM）を使う方法についてまとめます。

Author

Maple

Published

2025-08-30

Modified

2025-08-30

一般化加法モデルとは

一般化加法モデル（Generalized Additive Model; GAM）は、線形モデルの拡張版のようなもので、非線形な関係を捉えることができる柔軟な回帰モデルです。 GAMは、説明変数と目的変数の関係を滑らかな関数で表現し、複雑なデータ構造を扱うことができます。

GAMは、以下のような形式で表されます。

\[ g(E(Y)) = \beta_0 + f_1(X_1) + f_2(X_2) + ... + f_p(X_p) \]

ここで、$g$ はリンク関数、$E(Y)$ は目的変数の期待値、$\beta_0$ は切片、$f_i(X_i)$は説明変数 $X_i$ に対する滑らかな関数です。

RでGAMを使う

RでGAMを使うためには、mgcv パッケージを使用するのが一般的です。以下に基本的な使い方を示します。

パッケージのインストールと読み込み

install.packages("mgcv") # インストール（初回のみ）
library(mgcv) # パッケージの読み込み

データの準備

今回は、Rに組み込まれている mtcars データセットを使用します。

str(mtcars) # データの構造を確認

'data.frame':   32 obs. of  11 variables:
 $ mpg : num  21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
 $ cyl : num  6 6 4 6 8 6 8 4 4 6 ...
 $ disp: num  160 160 108 258 360 ...
 $ hp  : num  110 110 93 110 175 105 245 62 95 123 ...
 $ drat: num  3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
 $ wt  : num  2.62 2.88 2.32 3.21 3.44 ...
 $ qsec: num  16.5 17 18.6 19.4 17 ...
 $ vs  : num  0 0 1 1 0 1 0 1 1 1 ...
 $ am  : num  1 1 1 0 0 0 0 0 0 0 ...
 $ gear: num  4 4 4 3 3 3 3 4 4 4 ...
 $ carb: num  4 4 1 1 2 1 4 2 2 4 ...

11 個の変数が含まれています。ここでは、mpg（燃費）を目的変数、hp（馬力）、wt（車重）、cyl（気筒数）を説明変数として使用します。それぞれの変数の意味は以下の通りです。

mpg : Miles per gallon（燃費, 応答変数によく使われる）
hp : Horsepower（馬力, 連続）
wt : 車重（1000ポンド単位, 連続）
cyl : 気筒数（カテゴリ扱い可能）

データの可視化

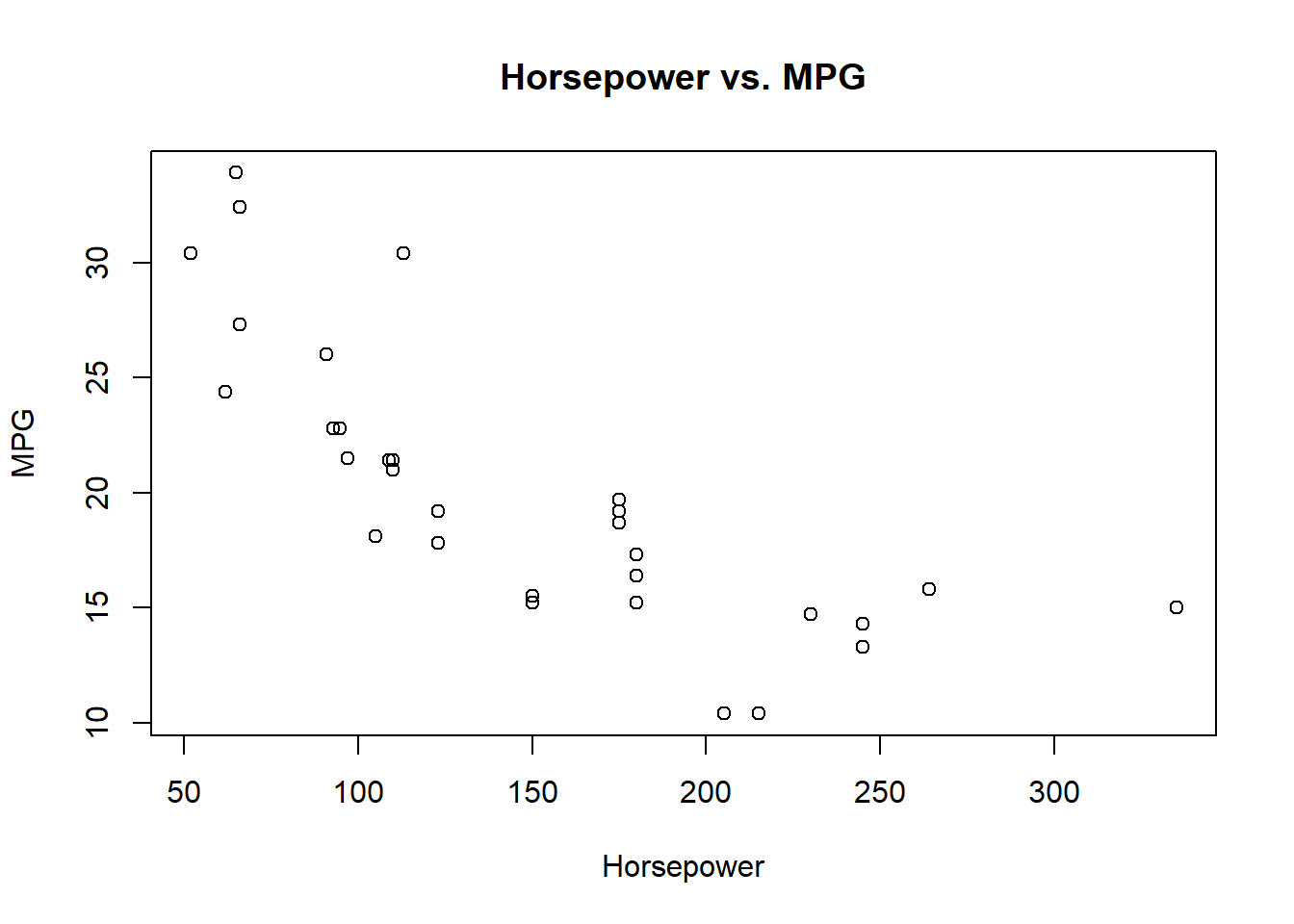
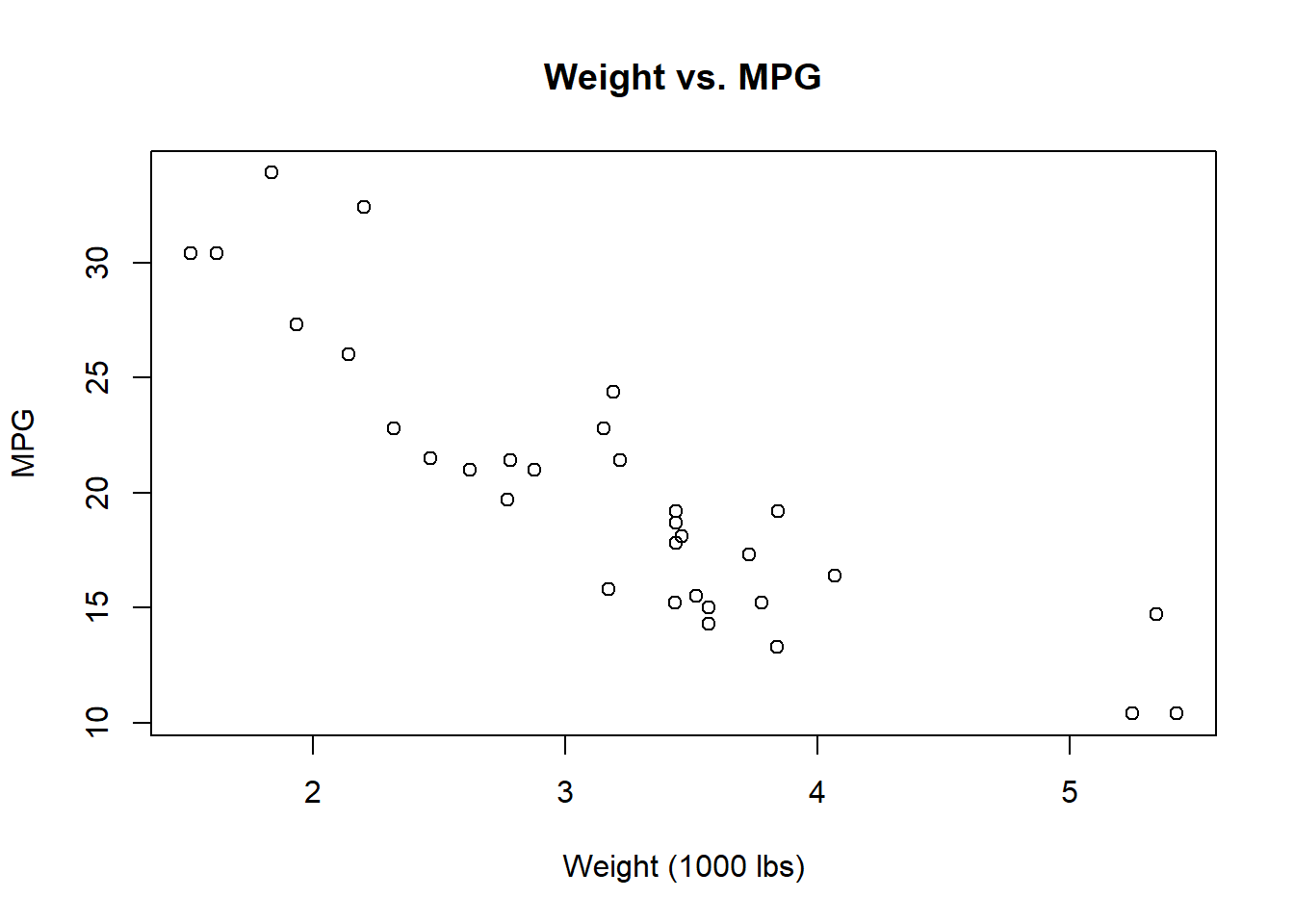
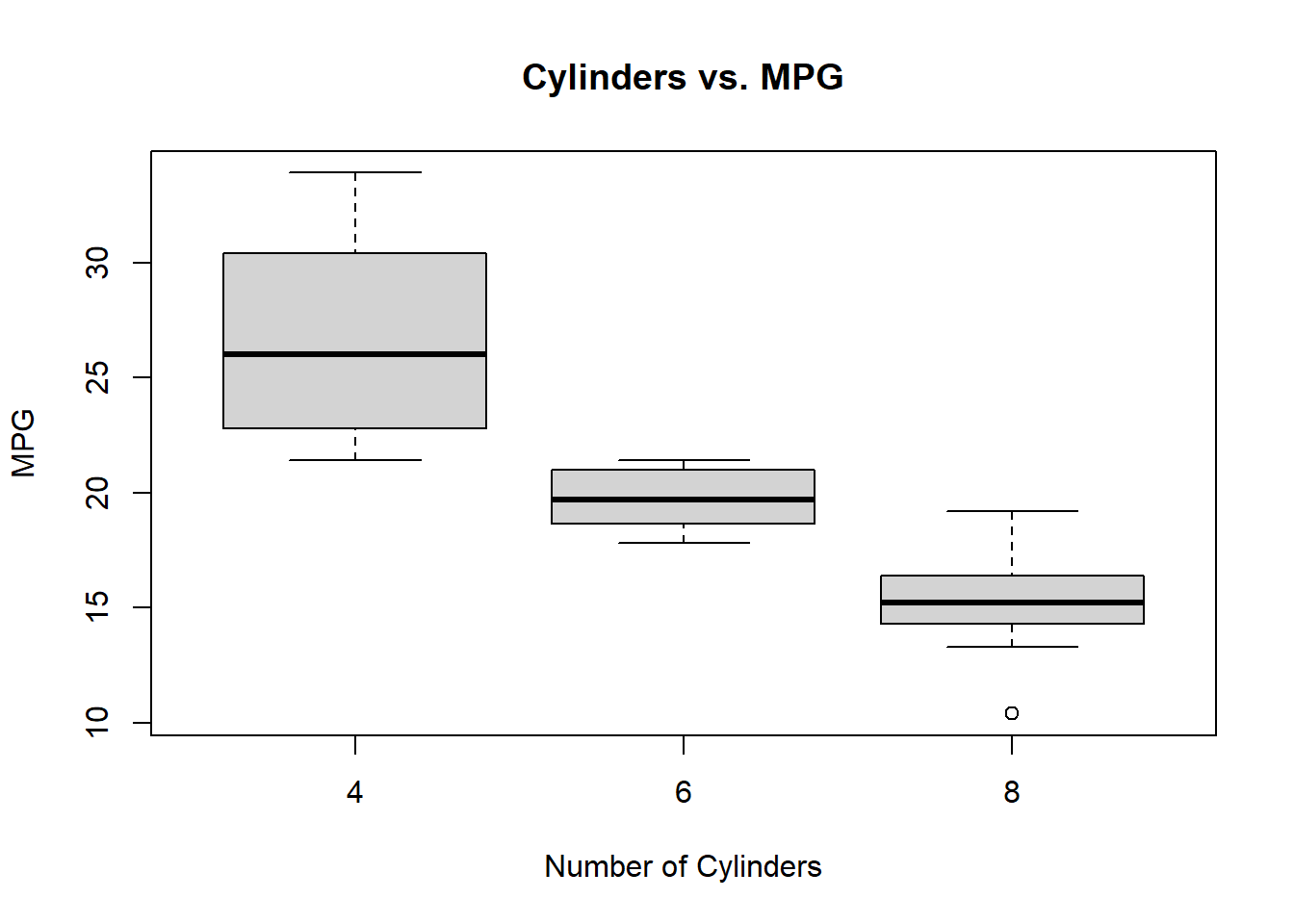
まずは、データを可視化してみます。どのデータも、まずは可視化が大事。

plot(
  mtcars$hp,
  mtcars$mpg,
  main = "Horsepower vs. MPG",
  xlab = "Horsepower",
  ylab = "MPG"
)

plot(
  mtcars$wt,
  mtcars$mpg,
  main = "Weight vs. MPG",
  xlab = "Weight (1000 lbs)",
  ylab = "MPG"
)

boxplot(
  mpg ~ cyl,
  data = mtcars,
  main = "Cylinders vs. MPG",
  xlab = "Number of Cylinders",
  ylab = "MPG"
)

いずれの変数も、増加すると mpg（燃費）が減少する傾向が見られます。しかし、単純な線形関係ではないように見えます。

cyl は箱ひげ図なのではっきりとはわかりませんが、hp と wt は非線形な関係がありそうです。

線形モデルの適用

まず、線形モデルを適用してみます。モデル作成には、lm() 関数を使用します。また、summary() 関数でモデルの結果を確認します。

model_lm <- lm(mpg ~ wt + hp + cyl, data = mtcars)
summary(model_lm)


Call:
lm(formula = mpg ~ wt + hp + cyl, data = mtcars)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.9290 -1.5598 -0.5311  1.1850  5.8986 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 38.75179    1.78686  21.687  < 2e-16 ***
wt          -3.16697    0.74058  -4.276 0.000199 ***
hp          -0.01804    0.01188  -1.519 0.140015    
cyl         -0.94162    0.55092  -1.709 0.098480 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.512 on 28 degrees of freedom
Multiple R-squared:  0.8431,    Adjusted R-squared:  0.8263 
F-statistic: 50.17 on 3 and 28 DF,  p-value: 2.184e-11

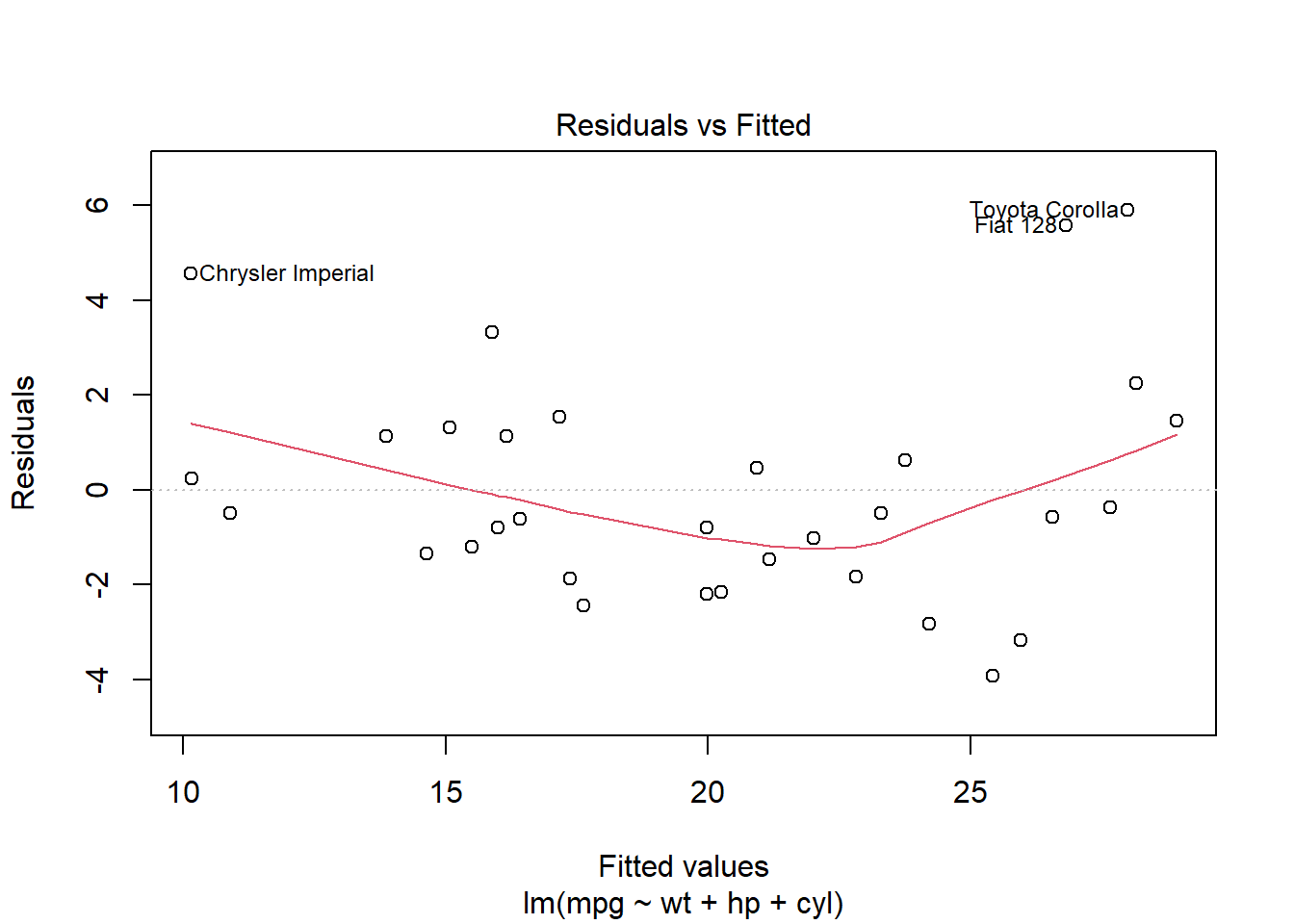
残差のプロットを確認します。 model_lm の残差がランダムに分布していない場合、非線形な関係が存在する可能性があります。

model_lm には4つのプロットが含まれています。 plot() 関数の which 引数でプロットの種類を指定できます。ここでは1つ目の残差 vs 予測値のプロットを確認します。

plot(model_lm, which = 1) # 残差 vs 予測値

残差はランダムに分布しておらず、U字型のパターンが見られます。このことから、非線形な関係が存在する可能性が示唆されます。

GAMの適用

次に、mgcv::gam() 関数で、GAMを適用してみます。

s(wt) で車重の非線形効果を捉えます
s(hp) で馬力の非線形効果を捉えます
factor(cyl) はカテゴリ（気筒数）の主効果を入れます

model_gam <- gam(
  mpg ~ s(wt) + s(hp) + factor(cyl),
  data = mtcars,
  medhod = "REML"
)
summary(model_gam)


Family: gaussian 
Link function: identity 

Formula:
mpg ~ s(wt) + s(hp) + factor(cyl)

Parametric coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)    20.982      1.352  15.520 2.58e-14 ***
factor(cyl)6   -1.450      1.524  -0.952    0.350    
factor(cyl)8   -1.311      2.366  -0.554    0.584    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
        edf Ref.df     F  p-value    
s(wt) 2.037  2.476 9.677 0.000453 ***
s(hp) 2.046  2.598 2.204 0.113295    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.869   Deviance explained = 89.5%
GCV = 6.1079  Scale est. = 4.7558    n = 32

Approximate significance of smooth terms:
        edf Ref.df     F  p-value    
s(wt) 2.037  2.476 9.677 0.000453 ***
s(hp) 2.046  2.598 2.204 0.113295

この部分に注目します。それぞれの意味は以下の通りです。

edf : 自由度（effective degrees of freedom）。1に近いほど線形に近く、2以上になると非線形な関係を示します。
Ref.df : 参照自由度。検定に使用されます。
F : F値。モデルの説明力を示します。
p-value : p値。0.05未満であれば、その変数が目的変数に対して有意な影響を与えていると判断します。

つまり、今回の結果の場合、wt は mpg に対して有意な非線形な影響を与えていることがわかります。一方、hp は有意ではないため、線形な関係で十分かもしれません。しかし、今回はデータ数が 32 と少ないため、慎重に解釈する必要があります。

また、今回はカテゴリ変数として入れている cyl については、平滑項ではなく、ダミー変数として扱われます。このため、edf は表示されず、Parametric coefficients: の部分に結果が表示されます。

Parametric coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)    20.982      1.352  15.520 2.58e-14 ***
factor(cyl)6   -1.450      1.524  -0.952    0.350    
factor(cyl)8   -1.311      2.366  -0.554    0.584

結果を見ると、cyl が 6 気筒または 8 気筒の車は、4 気筒の車に比べて mpg が低い傾向がありますが、有意ではない（p > 0.05）ではないことがわかります。しかし、サンプル数が少ないため、やはり慎重に解釈する必要があります。

ダミー変数について

今回、cyl はカテゴリ変数として扱っています。この場合、factor(cyl) とすることで、Rは自動的にダミー変数を作成します。

ダミー変数は、カテゴリ変数を数値化する方法の一つで、各カテゴリに対して0または1の値を割り当てます。例えば、cyl が 4, 6, 8 の3つのカテゴリを持つ場合、Rは以下のようなダミー変数を作成します:

factor(cyl)6 : cyl が 6 の場合は 1、その他の場合は 0
factor(cyl)8 : cyl が 8 の場合は 1、その他の場合は 0
基準カテゴリ（この場合は 4 気筒）は、両方のダミー変数が 0 の場合を表します

Rでは因子の 最初のレベル が基準になります（levels(factor(mtcars$cyl)) で確認可能）。このようにして、カテゴリ変数を回帰モデルに組み込み、係数は「基準と比べた差」を意味するようになります。

予測と可視化

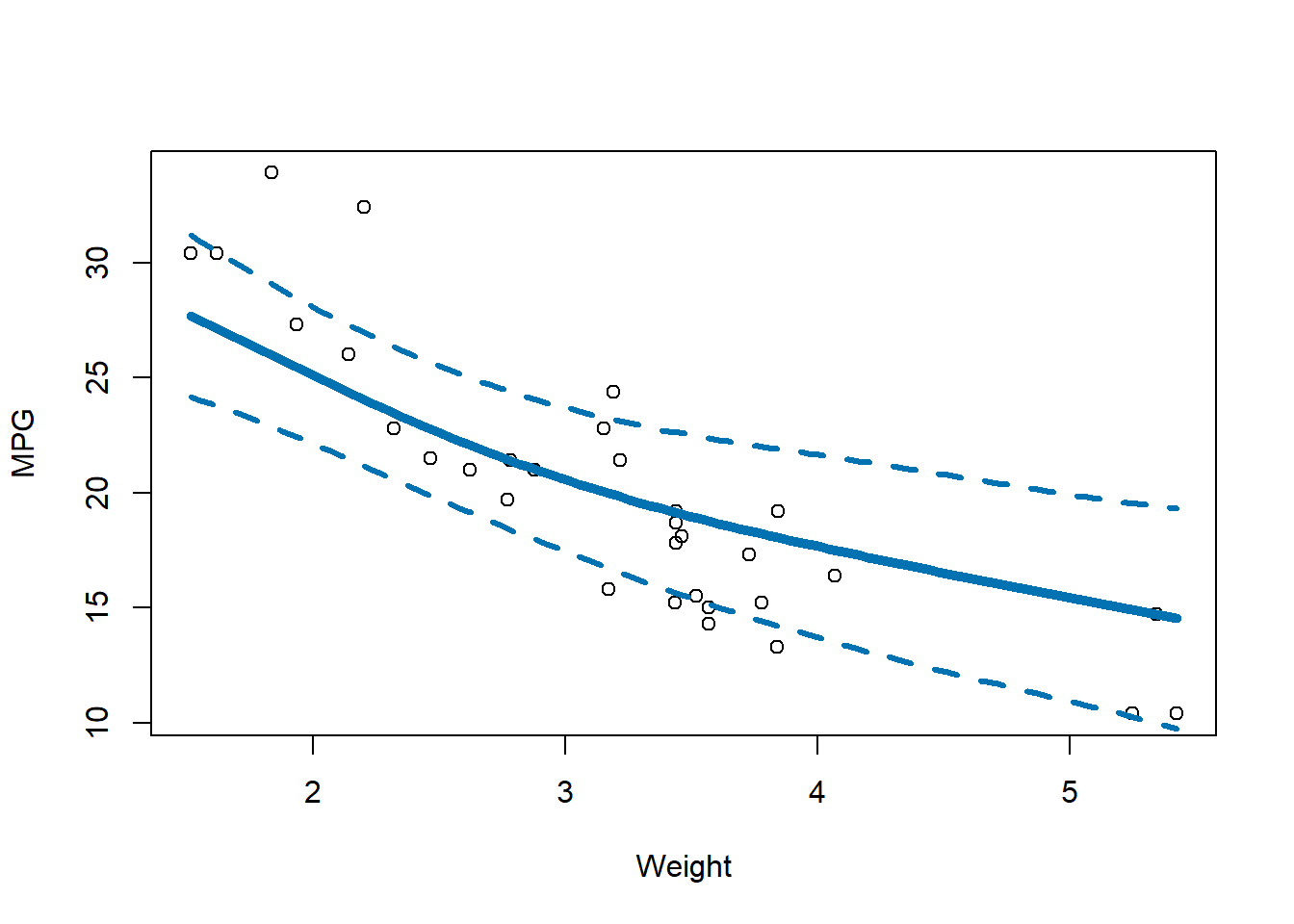
GAMモデルを使って予測を行い、結果を可視化してみます。今回、影響が有意だった wt に注目して、hp と cyl は平均値または最頻値で固定します。

palette("Okabe-Ito") # 色のパレットを設定
# 予測用の新しいデータフレームを作成
new_data <- data.frame(
  wt = seq(min(mtcars$wt), max(mtcars$wt), length.out = 100),
  hp = mean(mtcars$hp), # hpを平均値で固定
  cyl = as.factor(4) # cylを最頻値（4気筒）で固定
)
# 予測を実行
predicted_mpg <- predict(model_gam, newdata = new_data, se.fit = TRUE)
# 描画
plot(mtcars$wt, mtcars$mpg, xlab = "Weight", ylab = "MPG") # 元のデータを散布図で表示
lines(new_data$wt, predicted_mpg$fit, col = 6, lwd = 5) # 予測値の線を追加
# 推定値の95%信頼区間を追加
z <- qnorm(0.975) # 95%信頼区間のz値（約1.96）
lines(
  new_data$wt,
  predicted_mpg$fit + z * predicted_mpg$se.fit,
  col = 6,
  lty = 2,
  lwd = 3
)
lines(
  new_data$wt,
  predicted_mpg$fit - z * predicted_mpg$se.fit,
  col = 6,
  lty = 2,
  lwd = 3
)

結果のプロットを見ると、wt が増加するにつれて mpg が減少する非線形な関係が確認できます。

まとめ

一般化加法モデル（GAM）は、非線形な関係を捉えることができる柔軟な回帰モデルです。
Rでは、mgcv パッケージを使用してGAMを適用できます。
s() 関数を使って説明変数の非線形効果をモデルに組み込むことができます。
モデルの結果を解釈する際には、edf や p-value に注目します。
予測と可視化を通じて、モデルの適合度や関係性を理解することが重要です。

おまけ: グラフを見やすくする

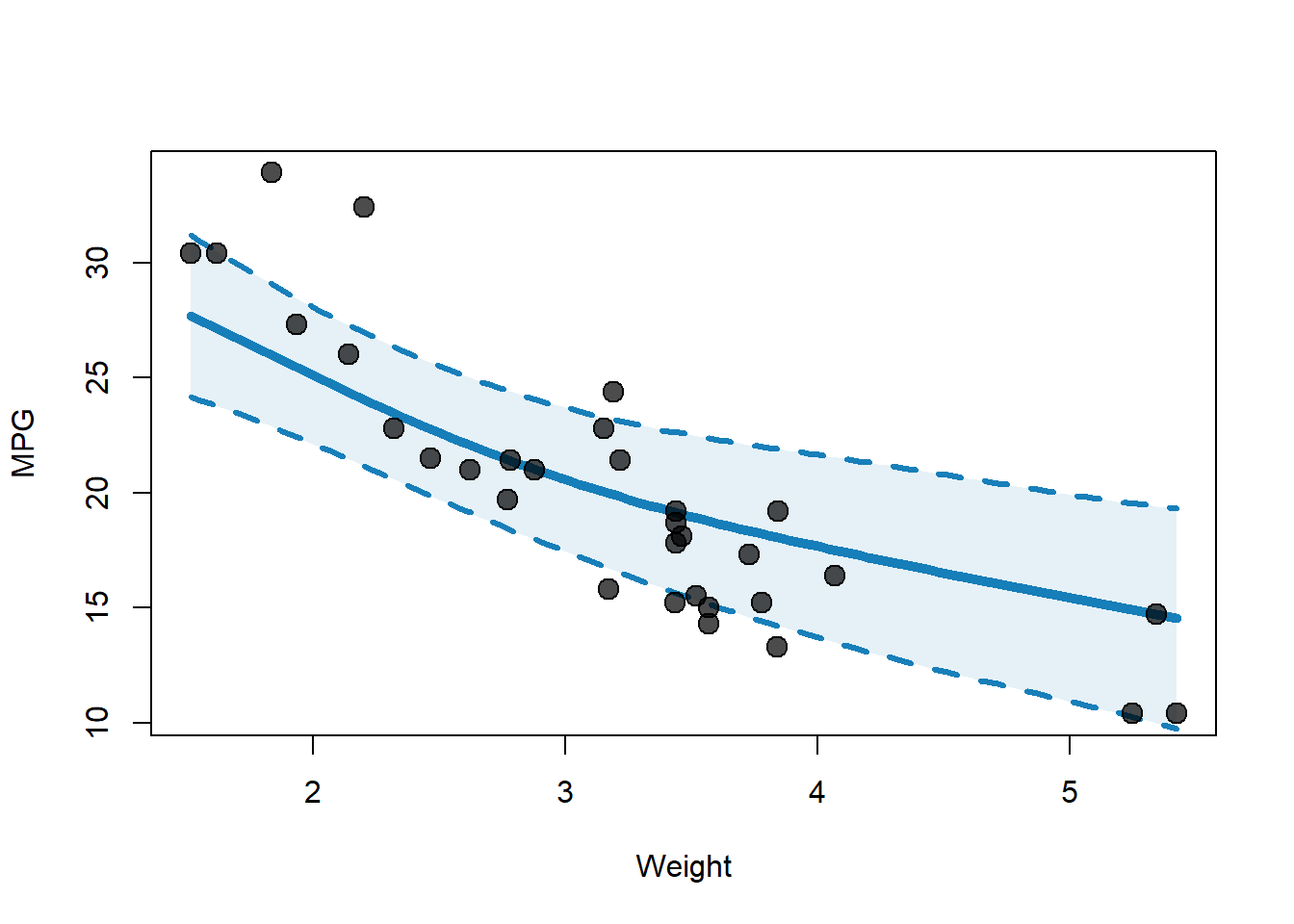
先ほどのグラフは最低限でしたが、もう少し見やすくするために、以下のような改善を加えることができます:

透過度を追加してデータポイントや線が重なっても見やすくする
信頼区間を塗りつぶしで表示する

透過度は、adjustcolor() 関数の alpha.f 引数で調整できます。また、塗りつぶしは、polygon() 関数を使用します。

palette("Okabe-Ito") # 色のパレットを設定
# 予測用の新しいデータフレームを作成
new_data <- data.frame(
  wt = seq(min(mtcars$wt), max(mtcars$wt), length.out = 100),
  hp = mean(mtcars$hp), # hpを平均値で固定
  cyl = as.factor(4) # cylを最頻値（4気筒）で固定
)
# 予測を実行
predicted_mpg <- predict(model_gam, newdata = new_data, se.fit = TRUE)
# 描画
plot(mtcars$wt, mtcars$mpg, xlab = "Weight", ylab = "MPG", type = "n") # 描画領域を準備
# 信頼区間を塗りつぶしで表示
z <- qnorm(0.975) # 95%信頼区間のz値（約1.96）
polygon(
  c(new_data$wt, rev(new_data$wt)),
  c(
    predicted_mpg$fit + z * predicted_mpg$se.fit,
    rev(predicted_mpg$fit - z * predicted_mpg$se.fit)
  ),
  col = adjustcolor(6, alpha.f = 0.1),
  border = NA
)
lines(
  new_data$wt,
  predicted_mpg$fit,
  col = adjustcolor(6, alpha.f = 0.9),
  lwd = 5
) # 予測値の線を追加
# 推定値の95%信頼区間を追加
lines(
  new_data$wt,
  predicted_mpg$fit + z * predicted_mpg$se.fit,
  col = adjustcolor(6, alpha.f = 0.9),
  lty = 2,
  lwd = 3
)
lines(
  new_data$wt,
  predicted_mpg$fit - z * predicted_mpg$se.fit,
  col = adjustcolor(6, alpha.f = 0.9),
  lty = 2,
  lwd = 3
)
# プロットを再描画して重ねる
points(
  mtcars$wt,
  mtcars$mpg,
  cex = 1.5, # プロットのサイズ
  pch = 21,
  col = adjustcolor(1, alpha.f = 0.9), # プロットの枠線の色
  bg = adjustcolor(1, alpha.f = 0.7) # プロットの塗りつぶしの色
)

参考

以下に、GAMに関する参考文献などをいくつか紹介します。

mgcv パッケージのドキュメント:
mgcv パッケージのCRANのドキュメントです。ここからリファレンスマニュアル（HTML版と PDF版）が読めます。
Generalized Additive Models: An Introduction with R, Second Edition:
mgcv パッケージの作者である Simon Wood 氏による書籍です。
An Introduction to Statistical Learning
GAMに限らず、RやPythonで統計解析をするための方法が記載されている教科書です。英語版は無料でPDFが公開されています。
- 日本語版は Rによる統計的学習入門です。